Oldschool - CONFidence Teaser 2019

Gynvael did a survey lately to see what kind of assembly is taught in Polish universities, and if any of them is still teaching the old 8086. Let us extend this question to the CTF scene!
This challenge is a clear reference to Gynvael's survey which is obvious from the description but it might be also a reference to a task that was part of Dragon Sector's CTF in 2018. There, the task was called Oldskul[1].
I still need to post a solution from that task too ;) ↩︎
What we get is a small gz file (646 B) and this is what we get when extracting its content.
➜ Oldschool ll
total 8.0K
-rwxrwxrwx 1 ubuntu ubuntu 344 Mar 15 14:21 flag.txt
-rwxrwxrwx 1 ubuntu ubuntu 1.1K Mar 13 23:55 oldschool.exe
-rwxrwxrwx 1 ubuntu ubuntu 646 Mar 29 17:55 oldschool_235e68c1b24b17463a010e8ca0d0ac2df0c4514286e0e490aabd1b25b8ae1168.tar.gz
Immediately visible flag.txt gives us something that it's not clearly understandable from the beginning.
➜ Oldschool cat flag.txt
4 { 4 p p
p { k 4 { E
p 4 4 p { p
4 p
S
%
Let's hope it will be more clear when we analyze the binary. Running file on the binary reveals that in fact this is an old school stuff - an MS-DOS Executable.
➜ Oldschool file oldschool.exe
oldschool.exe: MS-DOS executable
Let's try to run it an see what we get. We can't run it directly but for such situations we have DosBox.
After running DosBox we mount the folder that contains our files and execute it.
I would normally open this file in r2, but I've decided to give a Ghidra a try with this one. I had some experience with the tool before the CTF but it was just playing around so nothing too difficult.
Upon loading the binary in the Ghidra identifies the file as 16-bit in Real-mode.
This is in fact old. But not so old for me as my initial experience with ASM was in fact 16-bit in real mode. So seeing the code was only bringing back old memories (back in the days I was coding some stuff in ASM - you can find some of the work on my YT). So let's in fact look at the code.
After the initial analysis only 4 functions were created and one of them was entry so we being our exploration from there.
entry XREF[1]: Entry Point (*)
100f:0000 b8 24 10 MOV AX,0x1024
assume SS = <UNKNOWN>
assume SP = <UNKNOWN>
100f:0003 8e d0 MOV SS,AX
100f:0005 b8 90 01 MOV AX,0x190
100f:0008 8b e0 MOV SP,AXThe initial part sets up stack segment (SS) and pointer(SP). And after that prepars to display the string:
100f:000a b8 00 10 MOV AX,0x1000
100f:000d 8e d8 MOV DS,AX
100f:000f be 00 00 MOV SI,0x0
100f:0012 b4 09 MOV AH,0x9
100f:0014 ba a2 00 MOV DX,0xa2
100f:0017 cd 21 INT 0x21
If you are not familiar with DOS the it's worth to mention that application communicated with it with interrupts. The most useful one was (probably) 0x21. The standard was that you had to prepare some registers and in AH the operation number was passed. In this case we are setting to be AH=0x9 so we are going to display a string on screen.
Now it's a good time to find some resource on DOS interrupts. Back in the day the ultimate source was Ralf's Brows Interrupt List. You could find everything there. Of course you would have to have it downloaded first as internet access was not so common as nowadays. During this challenge there was only few method used so no comprehensive reference to DOS interrupts was needed. I've remember 0x9 (and few others) by heart.
So let's analyze the above part of code. In 0x9 command we need to pass the segment & offset to the string we want to display in DS:DX pair of registers. Segment registers cannot be set to literal value directly so we need to pass 0x1000 to DS indirectly via AX. DX points to the offset. So the string we want to display is located at: 0x1000:0xa2. Let's go there in Ghidra and see if we are correct:
1000:00a2 0a 47 69 ds "\nGive me a flag to draw!\n$ p4{krule_ctf}\nI
76 65 20
6d 65 20
Clearly we can see some text "Give me a flag to draw!\n", but it's looks like it's not terminated and Ghidra shows some more characters. This is in fact correct as the string that 0x9 command accept should be '$'-terminated. And we see the character there. So we get the first part of this CTF correctly. Next we have the call to FUN_100f_0058. Let's see what's there.
This method begins with something that looks like a preparation code and just after that we see another int 0x21 being used.
LAB_100f_0069 XREF[1]: 100f:0081 (j)
100f:0069 b4 01 MOV AH,0x1
100f:006b cd 21 INT 0x21
This time 0x1 is passed to AH and if we check any reference of this one we will get information that this is used to read character from STDIN. The character is returned in AL. We could now rename this method as read_flag (Ghidra uses L shortcut to open rename dialog box).
And this is consistent with the code we see next
100f:006d 3c 3a CMP AL,0x3a
1000:015f 72 37 JC LAB_100f_00a8
1000:0161 3c 47 CMP AL,0x47
1000:0163 72 45 JC LAB_100f_00ba
1000:0165 3c 67 CMP AL,0x67
1000:0167 72 37 JC LAB_100f_00b0
1000:0169 eb 49 JMP LAB_100f_00c4
This is clearly a bounds check code. We could right client on right side of CMP-s opcode and use a Convert sub-menu and then Char to actually instruct Ghirda to display it as a character instead of hexadecimal value. We will see the boundaries are set at: :, g or G. It might be not clear from the first sight but if we check ASCII table we get that ':' is right after digits and of course 'g' or 'G' is right after 'f' (and 'F') so it might be that this method accepts only hexadecimal digits as input. Let's verify that running the program again.
We can clearly see that going outside the valid range of hexadecimals stops the immediately but staying withing range allows us to go until the whole key is accepted.
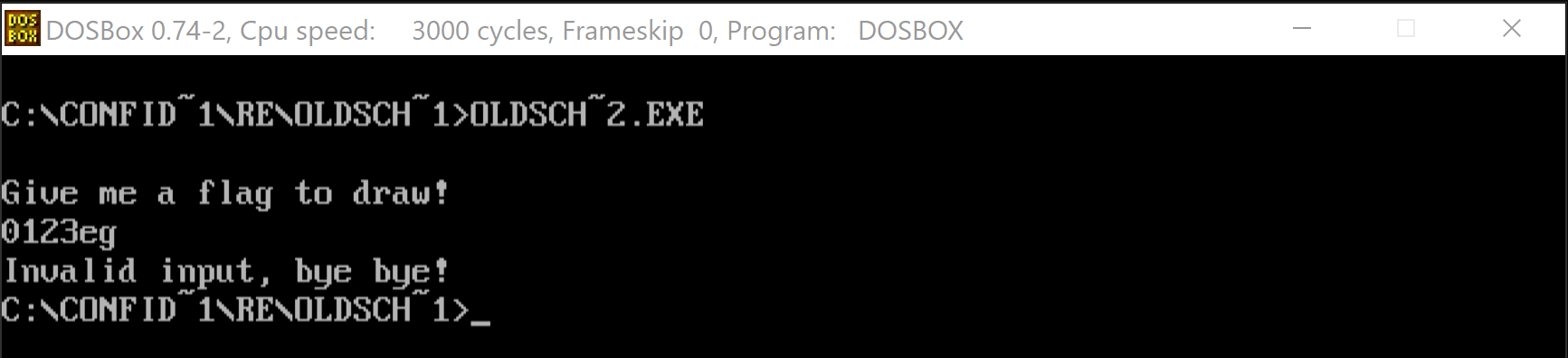
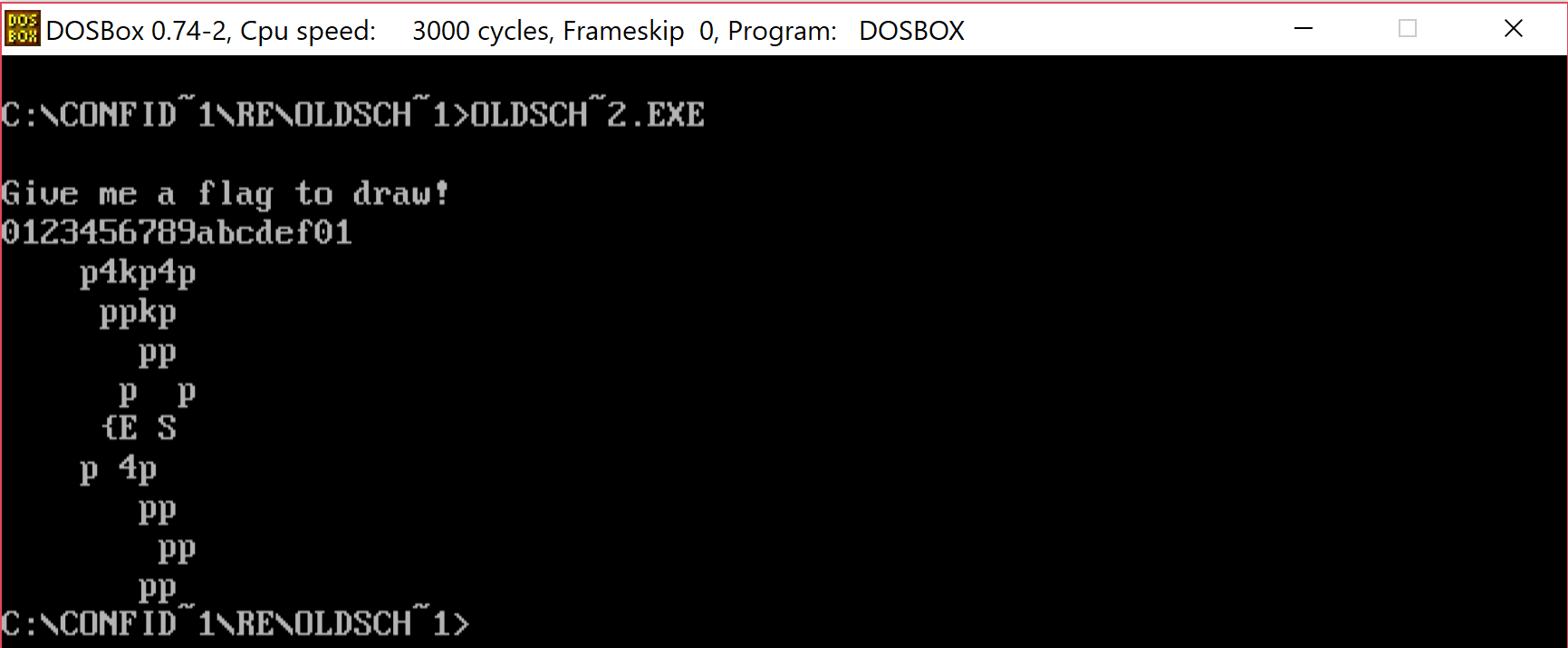
This looks a bit familiar to the stuff we saw in flag.txt. Let's try to see if we can find in this method a place where we display the text "Invalid input, bye bye!". That would confirm that we in fact correctly identified that it does.
100f:00c4 ba ca 00 MOV DX,0xca
100f:00c7 b4 09 MOV AH,0x9
100f:00c9 cd 21 INT 0x21
100f:00cb e9 62 ff JMP LAB_100f_0030Scrolling a bit further down we bump into already known operation - 0x9 with offset of the string set to be 0xca. And if we check an address of 0x1000:0xca we find our string. WooHoo!
Let's see if we can figure out what this function does with the characters it reads from the console.
If we look closer we notice there are too loops inside. The outer one that runs 9 times ( mov cx,09 @ 100f:005e) and the inner only 2 times ( mov cx, 02 @ 100f:0062). The inner part is rather easy to analyse and the core part is the following:
100f:007b f6 e3 MUL BL
100f:007d 02 d0 ADD DL,AL
In BL we have 0x10, AL contains the currently read character value (in hex) and DL previously calculated value. So this method just converts 2 read characters int a number in hex.
value = first_read_hex_char * 0x10 + secondly_read_hex_char
But that's not the end of this function. Right after we calculate the value there's another function that does some transformations. It's also a loop but this time we loop 4 times.
In those four iterations we can distinguish 3 phases.
LAB_1000_0176 XREF[1]: 100f:00a2 (j)
1000:0176 8a c2 MOV AL,DL
100f:0088 24 01 AND AL,0x1
100f:008a 74 63 JZ LAB_100f_00ef
100f:008c eb 7a JMP LAB_100f_0108
1st one is checking the lowest bit of the value from the user and jumping accordingly.
LAB_100f_008e
100f:008e 8a c2 MOV AL,DL
100f:0090 24 02 AND AL,0x2
100f:0092 74 3a JZ LAB_100f_00ce
100f:0094 eb 48 JMP LAB_100f_00de
2nd one is checking the bit no 1 and jumping to specific parts based if it's zero or not.
And the third part is shifting the value by 2 - that would correspond that we are done with the 2 bits and prepare for another two. Apart from that we see some array manipulation pointed by SI.
LAB_100f_0096
100f:0096 51 PUSH CX
100f:0097 b1 02 MOV CL,0x2
100f:0099 d2 ea SHR DL,CL
100f:009b 59 POP CX
100f:009c 8a 1c MOV BL,byte ptr [SI]
100f:009e fe c3 INC BL
100f:00a0 88 1c MOV byte ptr [SI],BL
We remember that what we get in AL is a byte of data and byte is 8x2bit so those manipulations are done on every 2bit element of provided byte. Ok, this is clear now what we are actually doing based on those bits and what is this thing pointed by SI.
If we check the address pointed by SI we can see there's a lot of empty space ( 0x00). There are four cases that we execute.
Based on bit-0:
bit_0_is_zero
100f:00ef bf 00 00 MOV DI,0x0
100f:00f2 3b f7 CMP SI,DI
100f:00f4 74 98 JZ check_bit_1
100f:00f6 8b c6 MOV AX,SI
100f:00f8 b3 12 MOV BL,0x12
100f:00fa f6 f3 DIV BL
100f:00fc 80 fc 00 CMP AH,0x0
100f:00ff 74 8d JZ check_bit_1
100f:0101 8b de MOV BX,SI
100f:0103 4b DEC BX
100f:0104 8b f3 MOV SI,BX
100f:0106 eb 86 JMP check_bit_1
bit_0_is_one
100f:0108 bf 00 00 MOV DI,0x0
100f:010b 3b f7 CMP SI,DI
100f:010d 74 0e JZ LAB_100f_011d
100f:010f 8b c6 MOV AX,SI
100f:0111 b3 12 MOV BL,0x12
100f:0113 f6 f3 DIV BL
100f:0115 80 fc 10 CMP AH,0x10
100f:0118 75 03 JNZ LAB_100f_011d
100f:011a e9 71 ff JMP check_bit_1
100f:011d 8b de MOV BX,SI
100f:011f 43 INC BX
100f:0120 8b f3 MOV SI,BXWe do here some additional checks but what the main part is doing is to add 1 (when bit 0 is 1) or subtract 1 (when bit 0 is 0) from SI.
For the bit number 1:
bit_1_is_zero
100f:00ce 8b de MOV BX,SI
100f:00d0 83 fb 11 CMP BX,0x11
100f:00d3 77 02 JA more_than_one_row
100f:00d5 eb 05 JMP LAB_100f_00dc
100f:00d7 83 eb 12 SUB BX,0x12
100f:00da 8b f3 MOV SI,BX
bit_1_is_one
100f:00de 8b de MOV BX,SI
100f:00e0 81 fb 8f 00 CMP BX,0x8f
100f:00e4 72 02 JC not_the_last_row
100f:00e6 eb 05 JMP last_row
100f:00e8 83 c3 12 ADD BX,0x12
100f:00eb 8b f3 MOV SI,BX
Here we just add 0x12 or subtract 0x12 based on the bit value. If we look at those index changes we see that this is moving to adjacent cells diagonally - 00 - NW, 01 - NE, 10 - SW and last 11 - SE. Lastly we mark the new visited cell by increasing the value that is stored in there.
So to sum up, in this method we read 9 hexadecimal values from the user. We look at each value as 4 separate 2-bit entries and we use those to compute new index in the table. The rules of converting the 2-bit are as follows
| bit 0/1 | 0 | 1 |
|---|---|---|
| 0 | NW | NE |
| 1 | SW | SE |
On entering the new field we add 1 to value stored there.
Just to confirm what we analyzed we can do a debugging session. I pulled some old Turbo Debugger (good old DOS times!) to see if it works as described above.
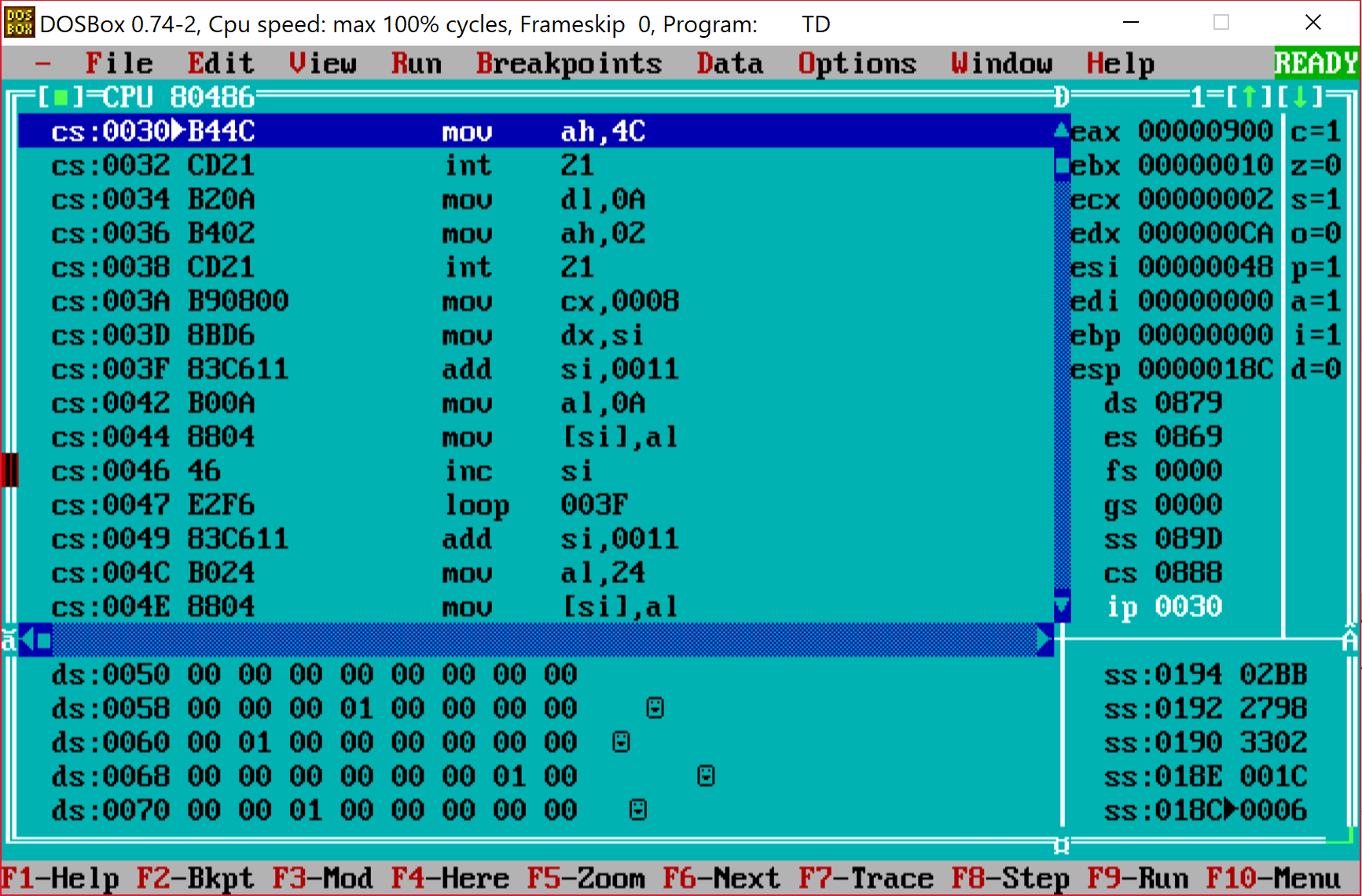
After few single steps we can see that in fact it behaves as we expected.
Function FUN_100f_0125 takes our array and a string p4{krule_ctf} (with a space at the front) and replaces entries in the array with a character located at the same position as the value in the cell. So if we walked certain cell once we will have character p (remember there's a space at the beginning of the string). If we visit it twice we will have 4 and so on. After the whole array checked we will end up with something like this (bottom part):
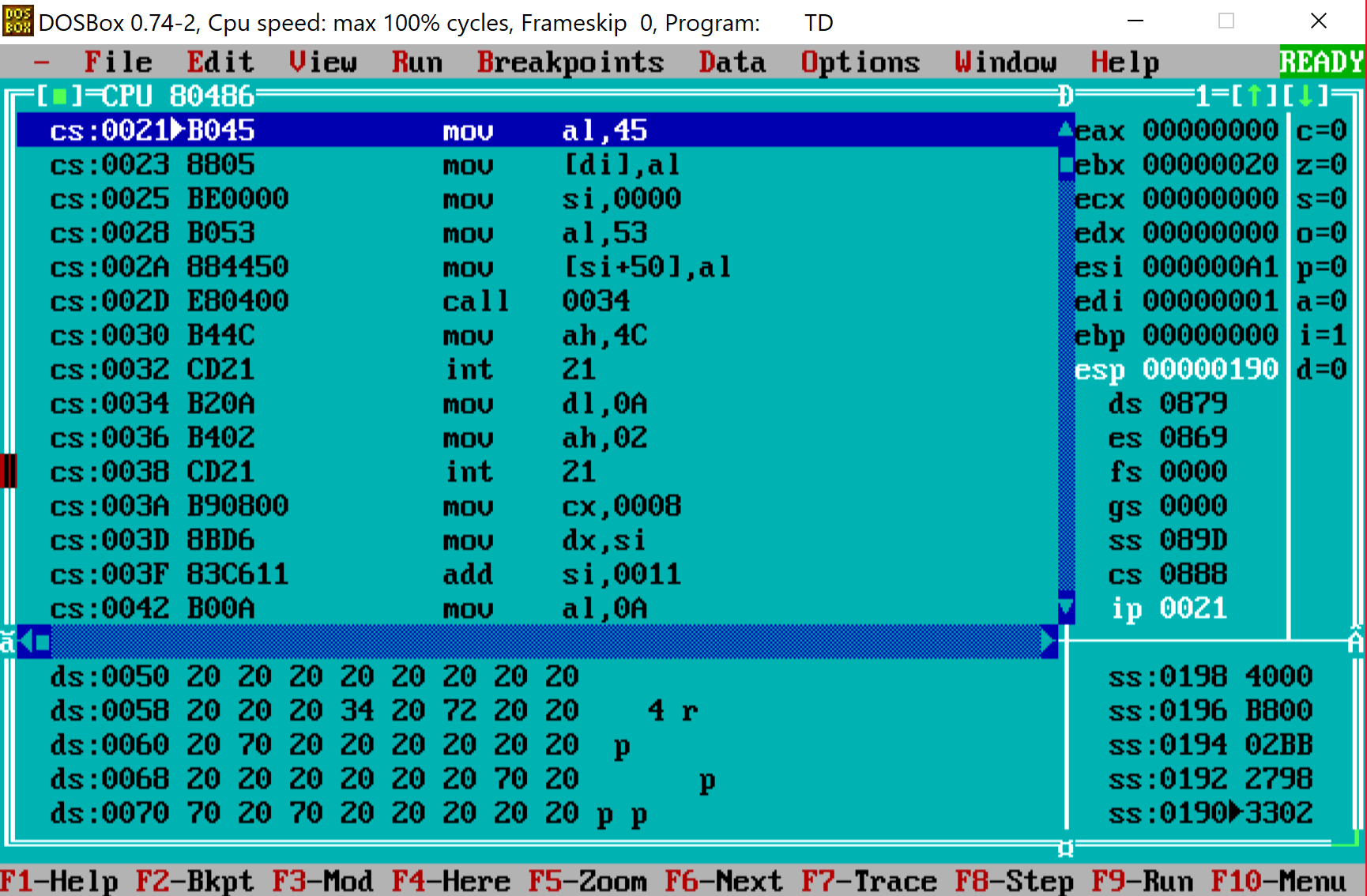
This is again, something that does look familiar. Remember what we get after entering valid hexadecimal characters and also what's in flag.txt? Ok, so our task is to "walk" through the table so that we cross each cell as many times so that when replaced the index with characters from p4{krule_ctf} will produce the same flag as the one in flag.txt. Now is the time to write some script.
We know that the initial value should be p4{ so we have our starting point.
bit_len=16
shifts=24
solution=[0x7b3470]
In my solution I've put that in a python script and include this in a main one. This way I was running script for next steps only and not run it once and got the final results. Easier to spot a problem (and I had few of those during coding).
String is converted into hex and reversed as this was it was easier to extract bits the same way as the original algorithm would do it.
The main script contains of the following:
1) The flag that we want to get at the end
original = [0,0,0,0,0,0,0,0,2 ,0,3,2,1,1,0, 0,
0,0,0,0,0,0,0,1,0 ,3,4,2,3,0,0xff,0,
0,0,0,0,0,0,1,0,2 ,2,1,3,0,1,0 ,0,
0,0,0,0,0,0,0,2,0 ,1,0,0,0,0,0 ,0,
0,0,0,0,0,0,0,0,0xfe,0,0,0,0,0,0 ,0]
Values in each cell indicates how many times we want to cross certain cell. 0xfe indicates starting position and 0xff is the cell where we should end.
After that we load the next solution from the file given as an input to this script:
import importlib
a=importlib.import_module(sys.argv[1])
And the main method for solving
The main idea is that we iterate through potential characters and add them to the list of potential solutions generated by the previous run. When we have what might be a solution we check if applying the algorithm over this input keeps us withing the boundaries - so that we do not cross any cell too many times. If so we add it to a lit of potential solutions but longer by one char. With such algorithm what we need to do is run the sequence of commands:
python solv.py sol3 > sol4.py
python solv.py sol4 > sol5.py
python solv.py sol5 > sol6.py
python solv.py sol6 > sol7.py
python solv.py sol7 > sol8.py
python solv.py sol8 > sol9.py
Each step runs gives us a new file with potential & partial solution that we feed into the script for next round. And after all, in sol9.py we have the list of potential flags. Since we started from p4{ all of them will have that quality but not all of them will end up with }. So we pick one that has 0x7d at the beginning (remember that they are reversed) and it was 0x7d31366269747b3470 and converting it to characters and reversing gave p4{tib61} and that was accepted as a flag.
The whole script can be found here. I hope you've enjoyed reading this - if you did share it. HF & GL
